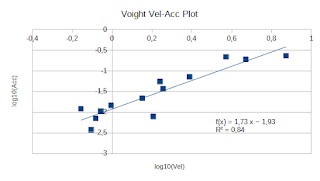
Ho ripreso in mano il discorso filtro Kalman applicato pero' a dati reali di un estensimetro (i dati sono espressi in decimi di millimetro)
import numpy as np
import matplotlib.pyplot as plt
dati = np.genfromtxt('est.csv', delimiter=';')
dist = dati[:,2]
z = dist.T
print(z)
dimensione = dist.shape
#print(dimensione[0])
n_iter = dimensione[0]
Q = 1e-5 # process variance
# allocate space for arrays
xhat=np.zeros(dimensione) # a posteri estimate of x
P=np.zeros(dimensione) # a posteri error estimate
xhatminus=np.zeros(dimensione) # a priori estimate of x
Pminus=np.zeros(dimensione) # a priori error estimate
K=np.zeros(dimensione) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect
x = 23.6
xhat[0] = 23.6
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1]
Pminus[k] = P[k-1]+Q
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R )
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k])
P[k] = (1-K[k])*Pminus[k]
sp = np.diff(xhat, prepend=xhat[0])
plt.figure()
plt.plot(z,'k+',label='noisy measurements')
plt.plot(xhat,'b-',label='a posteri estimate')
plt.legend()
plt.title('Kalman filter ', fontweight='bold')
plt.xlabel('Time')
plt.ylabel('Distance')
plt.figure()
valid_iter = range(1,n_iter) # Pminus not valid at step 0
plt.plot(valid_iter,Pminus[valid_iter],label='a priori error estimate')
plt.title('Estimated $\it{\mathbf{a \ priori}}$ error vs. iteration step', fontweight='bold')
plt.xlabel('Iteration')
plt.ylabel('$(Voltage)^2$')
plt.setp(plt.gca(),'ylim',[0,.01])
plt.figure()
plt.plot(sp,'b-')
plt.title('Speed', fontweight='bold')
plt.xlabel('Time')
plt.ylabel('Speed (0.1mm/day)')
plt.show()